شرح نظريتي ثايفنين ونوريتين خطوة بخطوة مع حاسبة وامثلة توضيحية
مبرهنة ثيفنين في تحليل دائرة دي سي
مهندس فرنسي، م.ل ثيفينين(M.L Thevenin) ، جعل واحدة من هذه القفزات النوعية في عام 1893. نظرية ثيفينين (المعروفة أيضا باسم نظرية هيلمهولتز-ثيفينين) ليست في حد ذاتها أداة تحليل، ولكن الأساس لطريقة مفيدة جدا لتبسيط الدوائر النشطة (active circuits) والشبكات المعقدة (complex networks). هذه النظرية مفيدة لحل الدوائر والشبكات الخطية المعقدة بسرعة وسهولة ، وخاصة الدوائر الكهربائية (electric circuits) والشبكات الإلكترونية.
Thevenin’s Theoremيمكن ذكر مبرهنة تفينين أدناه:
ايشبكة كهربائية خطيةأو دائرة معقدة ذات مصدر تيار وفولطية يمكن إستبدالها بدائرة مكافئة تحتوي على مصدر جهد كهربي مستقل واحدVTHوايظا على التوالي مع المقاومةRTH.
- VTH=Thevenin’sVoltage جهد ثيفينين
- RTH=Thevenin’sResistance مقاومة ثيفينين
خطوات تحليل دائرة كهربائية باستخدام نظرية تيفين :
1. افتح مقاومة الحمل.
2. حساب قياس فولطية الدائرة المفتوحة. هذا هو فولطية (Thevenin Voltage (VTH)) ثايفنين
3. فتح مصادر التيار ومصادر الجهد الكهربائي القصيرة(الشورت).
4. حساب قياس مقاومة الدائرة المفتوحة. هذه هي مقاومة تيفينين.
5. الآن، أعد رسم الدائرة بجهد كهربي داري مفتوح مقاس (open circuit Voltage (VTH)) في الخطوة (2) كمصدر للفولتية ومقاومة للدائرة المفتوحة المقاسة (Thevenin Resistance (RTH)) في الخطوة (4) كسلسلة مقاومة ونقوم بتوصيل مقاوم التحميل الذي قمنا بإزالته في الخطوة (1). هذه هي دائرة ثيفنين المناظرة لتلك الشبكة الكهربائية الخطية أو الدائرة المعقدة التي كان يجب تبسيطها وتحليلها بواسطة نظرية ثيفنين. لقد فعلت.
6. الآن إبحث عن التيار الكلي المتدفق من خلال مقاومة الحمل باستخدام قانون أوم (Ohm’s Law):
IT= VTH/(RTH+ RL).
مثال على نظرية ثيفينين:
مثال :
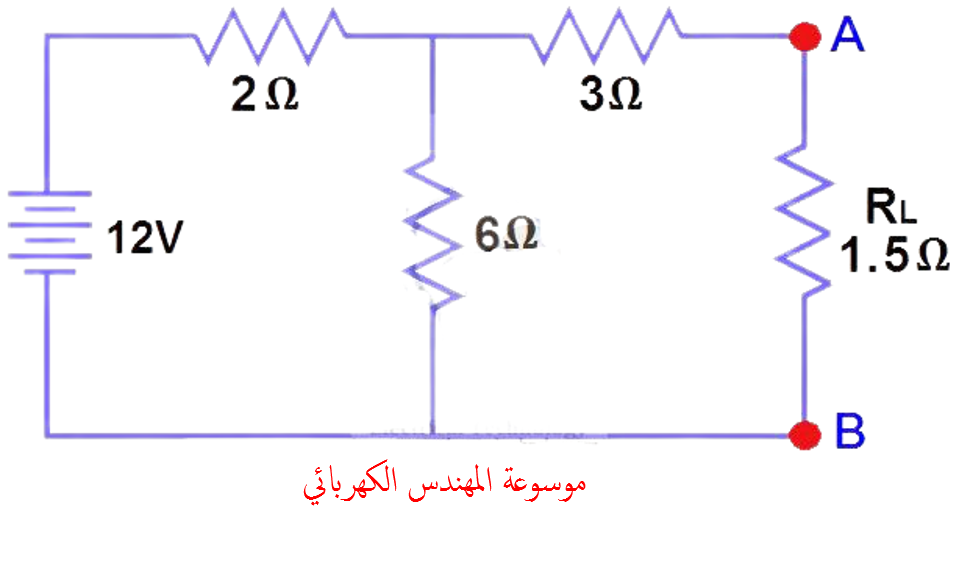
البحث عن (VTH, RTH) وتيار الحمل (IL) التي تتدفق من خلاله و جهد مسلط على مقاومة الحمل في الشكل (1) باستخدام نظرية تيفينين.by using Thevenin’s Theorem.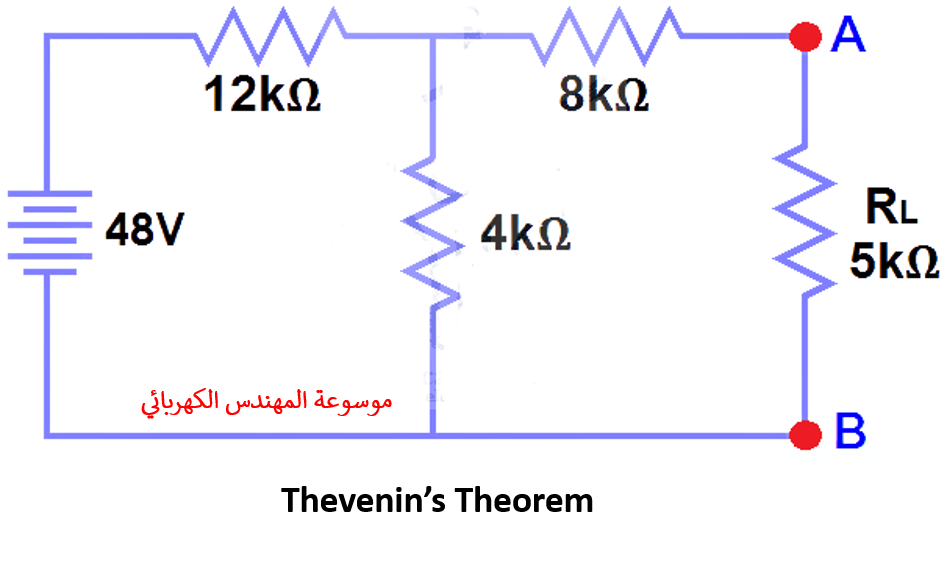
الحل :-
الخطوة 1 :
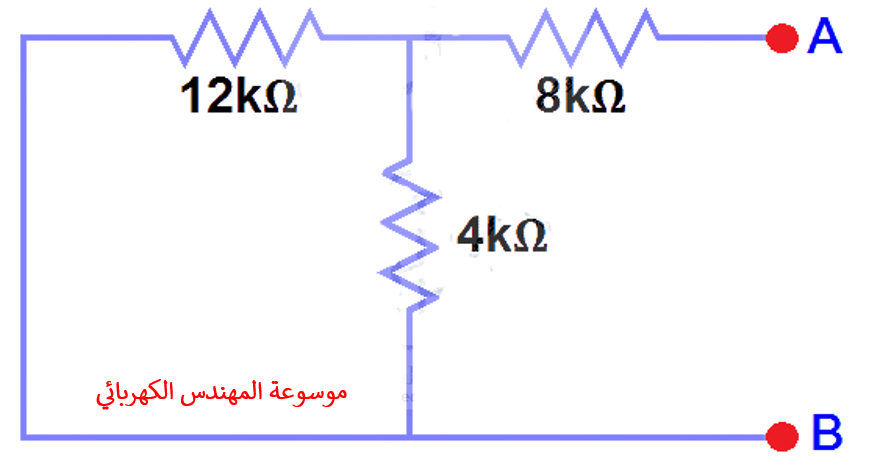
أفتح مقاومة الحمل (5kΩ load resistor) الشكل (2).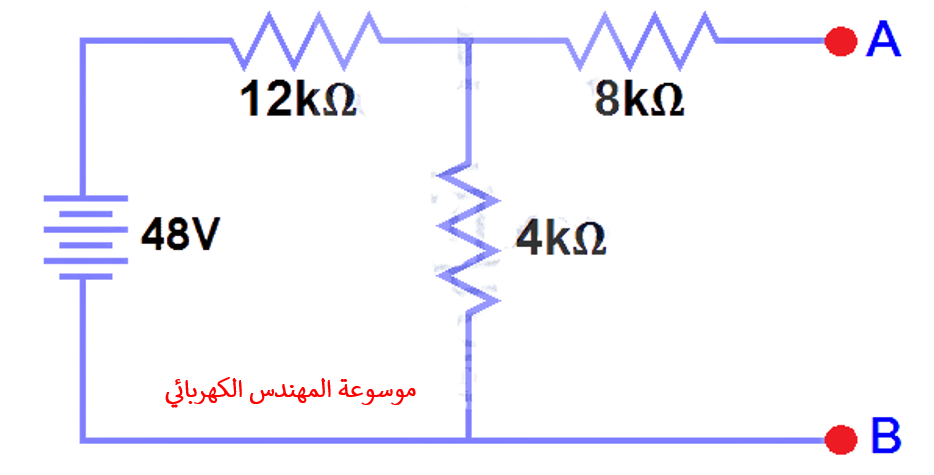
الخطوة 2:
حساب / قياس فولطية الدائرة المفتوحة. هذا هو فولطية ثايفنين (Thevenin Voltage (VTH)). الشكل (3).
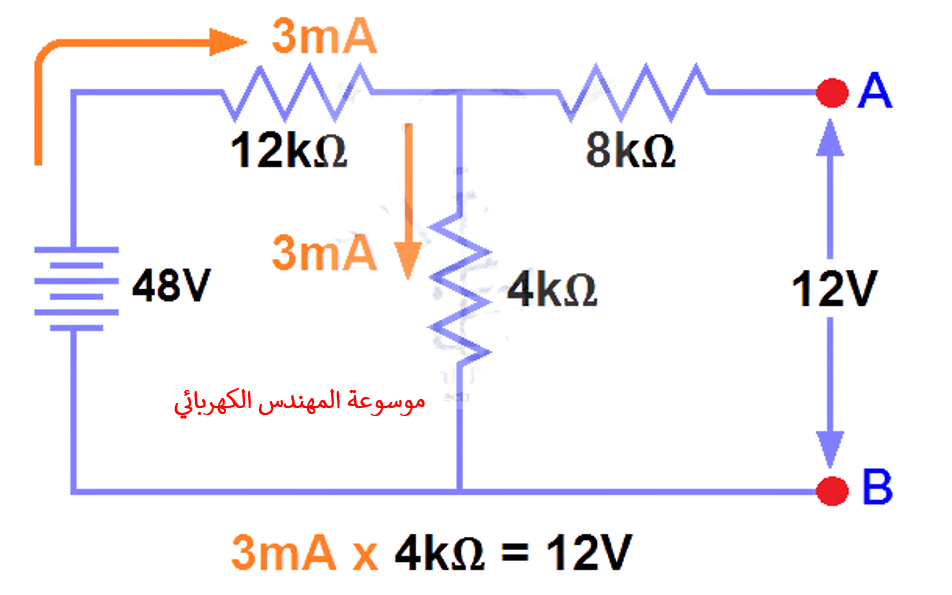
لقد أزلنا بالفعل مقاوم الحمل في الشكل 1، لذلك أصبحت الدائرة دائرة مفتوحة(open circuit) كما هو موضح في الشكل 2. الآن علينا حساب جهد ثيفنين. وسوف يتدفق تيار قيمتة3mAفي كل من مقاومات12kΩ,4kΩحيث أن هذه دائرة توالي والتيار لن يتدفق في المقاوم8kΩلان مقاومة مفتوحة .
وبهذه الطريقة،12V(3mA x 4kΩ)سوف تظهر عبر المقاومة4kΩ resistor. ونعلم أيضا أن التيار لا يتدفق من خلال مقاومة 8kΩ حيث أنها دائرة مفتوحة، لكن المقاوم ال 8kΩ متوازي (parallelwith4kΩ resistor) مع مقاومة4k resistor. وبالتالي فإن نفس الفولطية أي 12 فولت ستظهر عبر مقاومة 8kΩ وكذلك مقاومة 4kΩ . وبالتالي ستظهر 12 فولت عبر اطراف AB. أي
VTH= 12V
الخطوة 3 :
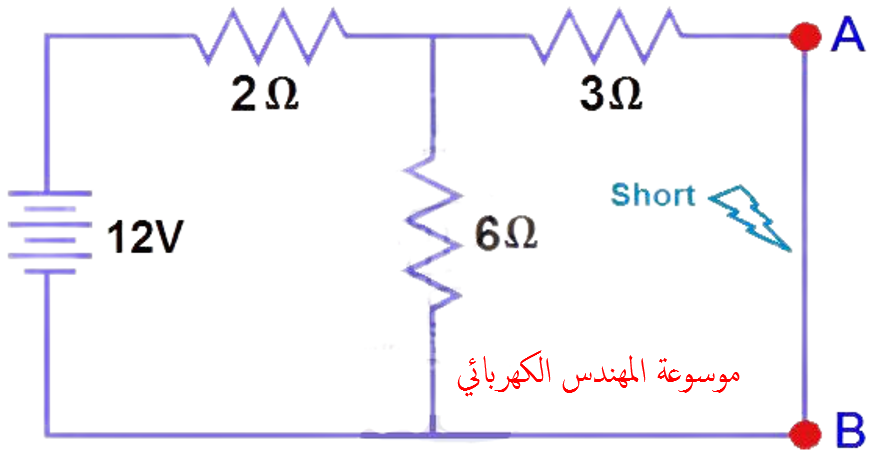
فتح مصدر التيار مصدر الجهد الكهربائي القصيرة(andshort voltage sources) كما هو موضح أدناه. الشكل (4)
الخطوة 4:
حساب / قياس مقاومة الدارة المفتوحة. هذه هي مقاومة ثايفنين (RTH).
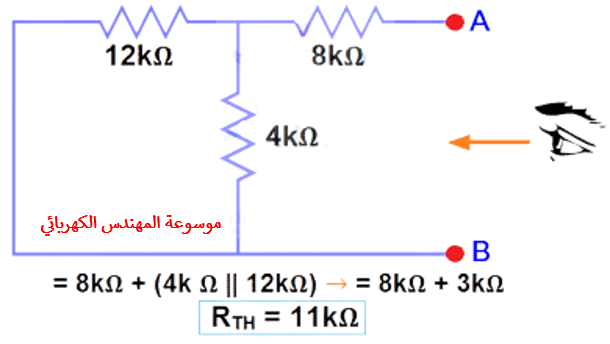
لقد قمنا بإزالة مصدر DC 48V اي الجهد في دائرة يساوي الصفر(48V DC sourcetozero) وذلك بعمل شورت على مصدر جهد او وضع سلك حول اطراف مصدر, كما موضح في الدائرة المكافئ أي 48V DC اصبح المصدر الجهد عبارة عن سلك (شورت سيركت) في الخطوة 3 (كما هو موضح في الشكل 3). يمكننا أن نرى أن المقاومة 8kΩ هي على التوالي مع توازي(parallel connection) المقاومات 12kΩ و 4kΩ . أي:
8kΩ + (4k Ω || 12kΩ) ….. (|| = in parallel with توازي مع)
RTH= 8kΩ + [(4kΩ x 12kΩ) / (4kΩ + 12kΩ)]
RTH= 8kΩ + 3kΩ
RTH= 11kΩ
الخطوة 5 :
قم بتوصيل RTHعلى التوالي مع الجهد ثايفنين VTHوإعادة توصيل مقاوم الحمل. يظهر هذا في الشكل(6) أي دائرة Thevenin مع مقاوم الحمل. هذه الدائرة المكافئة ل(ثايفنين).
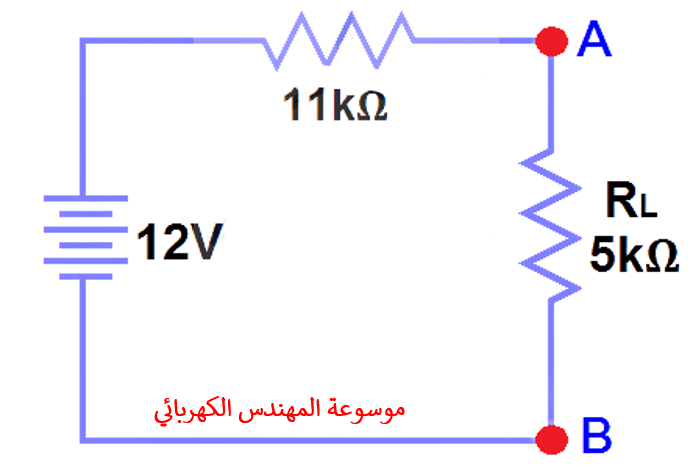
الخطوة 6 :
الآن تطبيق الخطوة الأخيرة أي قانون أوم (Ohm’s law). الان نحساب تيار الحمل الكلي والجهد الحمل كما هو مبين في الشكل 6.
IL= VTH/ (RTH+ RL)
IL= 12V / (11kΩ + 5kΩ) → = 12/16kΩ
IL= 0.75mA
And
VL= ILx RL
VL= 0.75mA x 5kΩ
VL= 3.75V
قارن الآن هذه الدائرة البسيطة مع الدائرة الأصلية المبينة في الشكل 1. هل ترى كم سيكون أسهل لقياس وحساب تيار الحمل في دائرة معقدة وشبكة لمقاومات(resistors) الحمل المختلفة من قبل نظرية ثايفنين؟ نعم وفقط نعم.





![{\displaystyle R_{\mathrm {eq =R_{1 +\left[\left(R_{2 +R_{3 \right)\|R_{4 \right)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/784a48e2f70421ddfc3e56b170f347a47510eb3b)
![{\displaystyle =1\,\mathrm {k \Omega +\left[\left(1\,\mathrm {k \Omega +1\,\mathrm {k \Omega \right)\|2\,\mathrm {k \Omega \right)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a0d92b2e21a89be84caa93e7b7caeecc562cbfc1)